last updated Dec 19, 1999

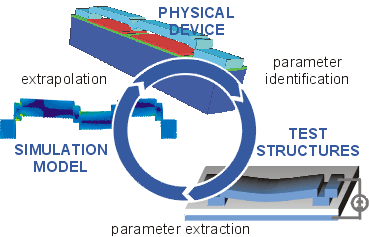
The goal is to characterize a fabrication process and calibrate a simulator to help a designer optimize device designs. We have a device that we want to build. First, we need to identify some basic parameters that determine the performance of this device such as geometry or shape, and material properties. Then we design test structures that isolate these parameters allowing accurate parameter extraction. All this information is stored in a detailed simulation model which can then be used to design or extrapolate the performance of the actual device. Straightforward enough but many engineers stop at various points along the wheel. Either they perform parameter extraction without going on to the design and extrapolation step, or perform simulations without using real extracted parameters, just hoping to get lucky. All the steps must flow consistently to be confident that we know what's really going on. 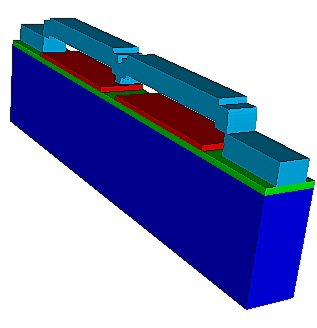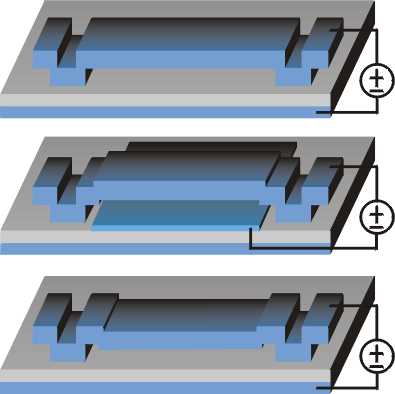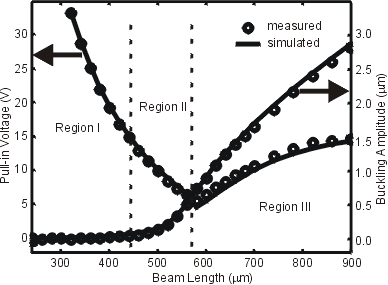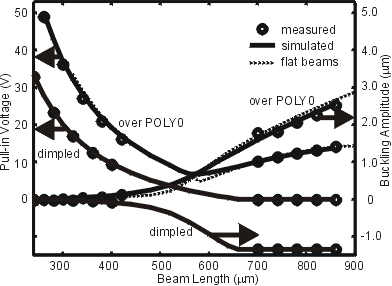Test Structures Fixed-fixed beams of various lengths are fabricated. Discontinuities - steps over POLY0, and dimples - are characterized explicitly. Buckling amplitudes are measured using an optical profilometer. Pull-in voltages are then measured using a CV meter. The boundary conditions are designed to be essentially 2D to match simulations better. 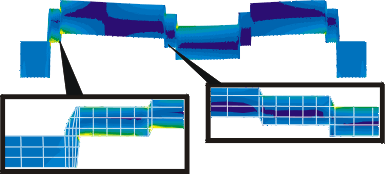Characterization of flat beams (table of data) Characterization of beams with discontinuities (table of data) Layout (GDS II or CIF) (click on picture for larger image)   Composite CAD Process Definition Specification   Simulation This two-dimensional computer simulation model capturing the various discontinuities forms a scalable simulation-based repository of process information. Geometry and material properties than can be passed on unambiguously to design engineers. This avoids the use of fudge factors which are rather specific and often cryptic. An electrostatic field subroutine that includes the effects of fringing and finite plate thickness is incorporated into Abaqus to convert it from a mechanical solver into an efficient coupled electromechanical solver. Given the current state of computers and software, this is the best tradeoff between accuracy and speed for characterization purposes. 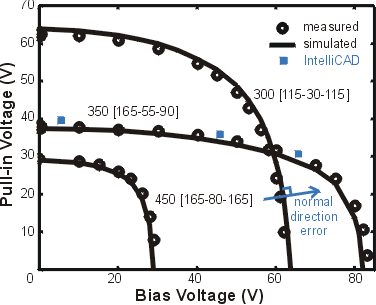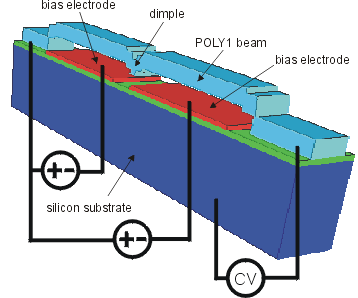Simulation parameters Measured Thicknesses (microns) POLY0 (with gold) 0.52 POLY0 (without gold) 0.53 POLY1 1.97 Dimple depth 0.67 Sacrificial PSG 1.79 Nitride (electrical) 0.077 Stepup sidewall 2.10 Extracted Properties Initial biaxial stress 6.3 MPa Young's modulus 140 GPa Simulated beam (Abaqus input decks) Extrapolation The well-calibrated simulation model is then used to predict the behavior of more complex dual-electrode structures. The voltage at one electrode required to pull the beam center onto the nitride is measured as a function of the bias voltage applied to the other electrode. The extrapolation is excellent confirming the validity of the extraction procedures and the viability of these measurements as benchmarks for coupled electromechanical simulators. Measured and simulated pull-in voltages (table of data)