Reduced order models consisting of one, two or several coupled Ordinary Differential Equations are often used to understand the behavior of electrostatically actuated devices when three-dimensional or even detailed two-dimensional models are too computationally intensive. These systems of ODEs are solved in Matlab, giving useful results that explain the general behavior of devices. 1D model of Micromachined Microwave Switch Jan 30, 1997 The micromachined switch has great potential for microwave applications due to its extremely low intermodulation distortion and IC backend technology compatibility. In the past, the switch has been modeled as a parallel plate capacitor attached to a linear spring at static equilibrium. 3D finite element simulations have been used to examine more detailed geometrical effects but are computationally expensive and mostly limited to static or quasi-static analyses. We have formulated a non-linear dynamic lumped model which models the support cantilevers and membrane separately and includes the effects of inertia, viscoelasticity, the external actuating circuit and residual stress. Parameter extraction for the lumped model from electrical measurements is described. Scaling properties for the geometrical design of the switch are analyzed. The modern design and performance optimization of micromachined switches deviates significantly from the simple geometry of cantilevers. The electrostatic force on the top diaphragm is so inhomogeneous that the approximation of a thin diaphragm anchored at the periphery under constant pressure is not accurate. It is more accurate and scalable to formulate the lumped model as a rigid diaphragm suspended above a ground plate by two cantilevers. The following figure shows the various geometrical parameters in the lumped model. 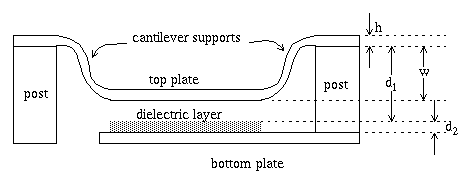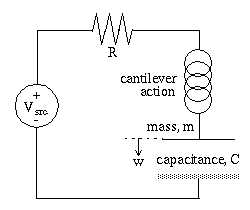This switch is controlled by an actuating circuit. A simple configuration is shown below. 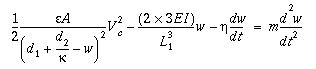The equation of motion of the center of the gap can be approximated by The first term on the left describes the total downward electrostatic force acting on the diaphragm. The second term describes the upward force exerted by the cantilevers and is valid when the vertical deflection is less than 30% of the cantilever length. The third term captures the effects of energy loss through cyclical plastic deformation, molecular friction and the viscosity of air via a viscoelasticity coefficient. The damping effect will reduce switch oscillation especially during switching off. 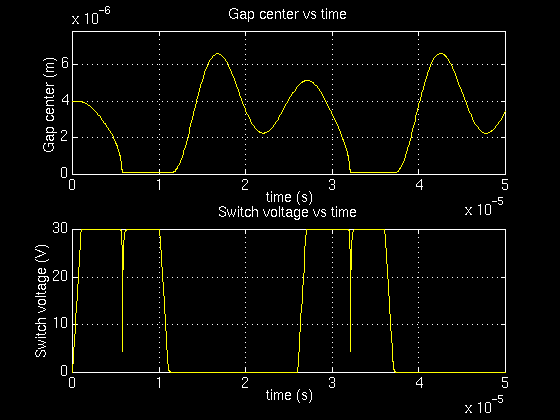The performance of the switch through two on-off cycles is shown below. The turn-on (closing of switch) response is strongly influenced by the position and direction of the diaphragm during its preceding turn-off oscillation. The two material parameters required by the model are the modulus of elasticity, E, and the viscoelasticity constant, n. Values of E for certain thin films can be measured but n is very difficult to determine. Since it is relatively easy to control R and Vsrc, parameter extraction can be accomplished by a least-squares fitting of the simulated transient characteristics to measurements with varying R and Vsrc. The following figure shows the turn-on time as a function of Vsrc for different values of E. 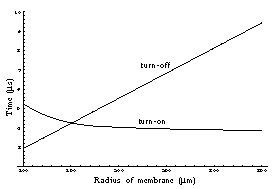After the material parameters have been determined, the model can be used to perform scaling studies of the geometry for performance optimization. The variation of switching times as a function of diaphragm radius is shown below. 2D model of micromachined RF switch Feb 11, 1997 The 1-D model of the micromachined RF switch is insufficient to capture some second-order effects. Here we describe a quasi-2D model of the switch that allows us to simulate the effects of distributed material parameters, and contact characteristics. The switch was discretized into 90 segments -- 54 segments for the center diaphragm and 18 segments each for the cantilevers. The cantilevers are 30um long and 5um wide whereas the diaphragm is 100um long and 200um wide. The electrostatic force, with a correction term for fringing effects, was applied only to the diaphragm. The animation shows one ON-OFF cycle of the switch which takes about 5us. 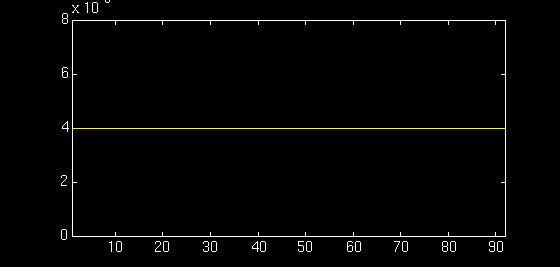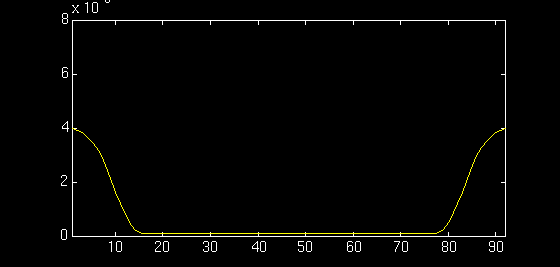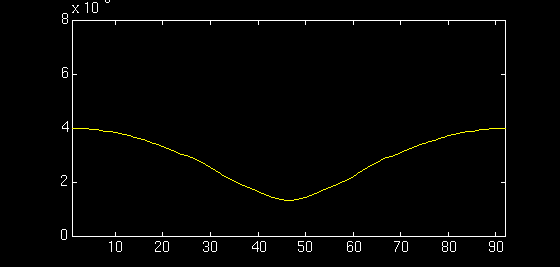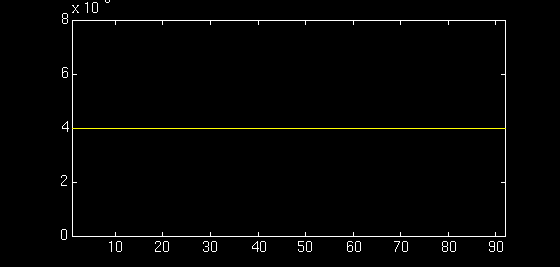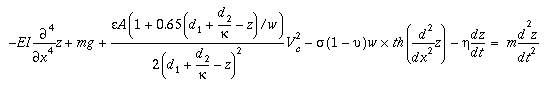The equation of motion of the cantilever and diaphragm can be approximated by The first term on the left describes the flexure of a beam whereas the second term is gravity. The third term is the electrostatic force with the fringing correction term. Residual stress is included in the fourth term while damping is accounted for in the fifth term. The quasi-2D distributed model allows for variations in width, thickness, and material parameters along the cantilevers and diaphragm. Residual stress can also be included as an additional stiffness constant. Stiction on contact is modeled as a barrier force that prevents the diaphragm from lifting off if the lifting force is insufficiently large. The contact of the diaphragm with the bottom dielectric layer is modeled as a perfectly inelastic collision -- the part of the diaphragm that hits the dielectric layer stops immediately and completely. Thus, a shock wave is generated that propagates through the cantilevers to the side supports. Further work is required to integrate the 1-D, quasi-2D, quasi-3D and full-3D models into a consistent hierarchical simulation. The viscoelasticity, and residual stress constants need to be verified.