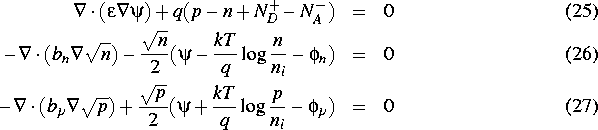
The ``silicon_dg3'' system solves for the three equation density gradient model.
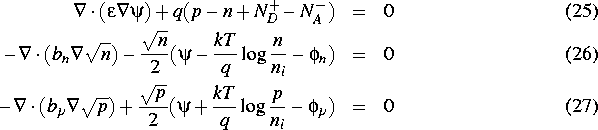
The solution variables for the above three equations are
![]() ,
, ![]() , and
, and ![]() ,
respectively. The physical constants
,
respectively. The physical constants ![]() and
and ![]() are defined as:
are defined as:


where l can be considered to be either the space dimensionality or
a fitting parameter; ![]() (
( ![]() ) is the electron (hole)
effective mass.
) is the electron (hole)
effective mass.
The silicon_dg3 system can only be used in situations in which no currents are flowing. It is most often used to obtain the initial solution at zero bias to be used in a subsequent silicon_dg5 calculation, for example. However, silicon_dg3 can also be used with applied bias for certain structures, such as a 1-D MOS capacitor. In that case, the most convenient approach is use a different material (e.g., poly) for the gate, and then set the following dbase parameter as follows:
dbase create name="/options/modulate_qf_with_bias" sval=''poly''This dbase entry will set the fixed quasi-Fermi level of the poly equal to the bias applied to the electrode in the bias statement.
Required Field Definitions
This system requires netdope to be defined after the structure is created with grid and deposit statements.
system name=silicon_dg3
+ sysvars=psi,sqrt_n,sqrt_p,ex
+ term0=ndiv_fbm.lapflux(psi|psi)@{silicon,poly,oxide}
+ term1=nodal.nscd(electrons,holes,netdope|psi)@{silicon,poly}
+ term2=dirichlet.dg_dirichlet(netdope|psi)@{silicon/gate,poly/gate,silico
n/back,silicon/source,silicon/drain,oxide/gate,silicon/substrate}
+ term3=constraint.continuity(psi|psi)@{silicon/oxide,poly/oxide}
+ term4=ndiv_fbm.diffusion(bn,sqrt_n|sqrt_n)@{silicon,poly}
+ term5=-0.5*nodal.prod(sqrt_n,phin|sqrt_n)@{silicon,poly}
+ term6=ndiv_fbm.diffusion(bp,sqrt_p|sqrt_p)@{silicon,poly}
+ term7=0.5*nodal.prod(sqrt_p,phip|sqrt_p)@{silicon,poly}
+ term8=dirichlet.default_dirichlet(0|sqrt_n,sqrt_p)@{silicon/oxide,poly/o
xide}
+ term9=-1.602e-15*interface.copy(stchg|psi)@{silicon/oxide,poly/oxide}
+ term10=nodal.copy(ex|ex)@{silicon,poly,oxide}
+ term11=dnodal.deriv_x(psi|ex)@{silicon,poly,oxide}
+ tmpvars=electrons,holes,phin,phip,bn,bp
+ func0=prod(sqrt_n,sqrt_n|electrons)@{silicon,poly}
+ func1=prod(sqrt_p,sqrt_p|holes)@{silicon,poly}
+ func2=phiMB(electrons,psi,tl|phin)@{silicon,poly}
+ func3=phiMB(holes,psi,tl|phip)@{silicon,poly}
+ func4=6.35e-9*inverse(mn|bn)@{silicon,poly}
+ func5=6.35e-9*inverse(mp|bp)@{silicon,poly}