In a semi-discrete finite element approach, space is discretized using a finite element method, resulting in a system of ODEs. This technique is illustrated using the following multi-dimensional diffusion initial boundary-value problem (IBVP). The diffusion coefficient is assumed to be a function of the impurity concentration.
The concentration of the
impurity is an unknown function of space and time ( ![]() ) on a domain (
) on a domain ( ![]() ). The strong
form (S) of the PDE model is
). The strong
form (S) of the PDE model is
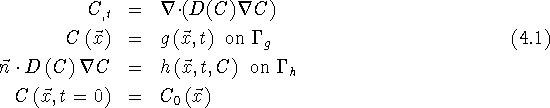
Note that it is not necessary to have a Dirichlet boundary
( ![]() ) for well-posedness. Also, for notational
simplicity, D(C) will usually be given as D, even though it
depends on C. For the present, we assume that the domain and
boundary conditions are fixed (i.e.
) for well-posedness. Also, for notational
simplicity, D(C) will usually be given as D, even though it
depends on C. For the present, we assume that the domain and
boundary conditions are fixed (i.e. ![]() does not change over
time nor do the the boundaries where
does not change over
time nor do the the boundaries where ![]() and
and ![]() are
applied).
are
applied).
This PDE model will be transformed to an equivalent semi-discrete
weak form of the problem by multiplying by a spatially varying
weighting function and integrating over the domain ( ![]() ). Two
classes of functions will be introduced. The first represents
possible solutions (trial functions) for the concentration, and the
strong form requires that this function space must be restricted by
). Two
classes of functions will be introduced. The first represents
possible solutions (trial functions) for the concentration, and the
strong form requires that this function space must be restricted by
![]() on
on ![]() . The second
represents allowable functions for the weighting space (test
functions), and it is restricted by the homogeneous counterpart of
the trial space (
. The second
represents allowable functions for the weighting space (test
functions), and it is restricted by the homogeneous counterpart of
the trial space ( ![]() on
on ![]() ). Continuity
constraints in the weak form will add additional restrictions to
these function spaces. The transformation from strong to weak form
proceeds as follows:
). Continuity
constraints in the weak form will add additional restrictions to
these function spaces. The transformation from strong to weak form
proceeds as follows:
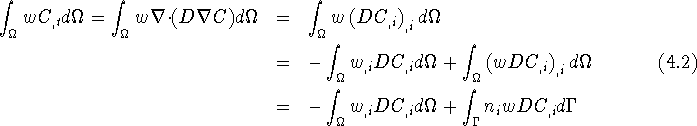
Note the use of Einstein notation ( ![]() ) for taking derivatives
with respect to an arbitrary number of spatial dimensions.
) for taking derivatives
with respect to an arbitrary number of spatial dimensions.
The trial and test function spaces are constrained as a result of
this weak form. Because of the first order derivatives in the weak
form, both the test and trial spaces must be first order continuous
(i.e. ![]() ) over the domain. Thus, the test and trial spaces are
) over the domain. Thus, the test and trial spaces are
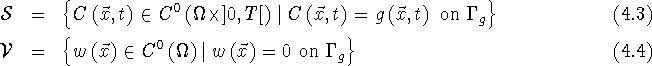
The weak form (W) of the problem follows directly. Find
![]() such that, for all
such that, for all ![]() ,
,
![]()
A mesh is introduced consisting of a set of elements ( ![]() )
and a set of nodes (
)
and a set of nodes ( ![]() ). The mesh is a simple tessellation of
the domain (i.e.
). The mesh is a simple tessellation of
the domain (i.e. ![]() and
and
![]() for
for ![]() ). The trial and test function
spaces are restricted to interpolations on this mesh (i.e.
). The trial and test function
spaces are restricted to interpolations on this mesh (i.e. ![]() and
and ![]() ). Note that introducing this interpolation may
violate
). Note that introducing this interpolation may
violate ![]() , as the interpolation is not exact,
but
, as the interpolation is not exact,
but ![]() is assumed to match
is assumed to match ![]() as closely as possible along
the prescribed boundary to minimize the impact of this violation.
The Galerkin FEM approximation (G) of the weak form follows. Find
as closely as possible along
the prescribed boundary to minimize the impact of this violation.
The Galerkin FEM approximation (G) of the weak form follows. Find
![]() such that, for all
such that, for all ![]() ,
,
![]()
Choose a basis for the set of interpolation functions on the mesh
such that the value of a function in this basis is 1 at the node it
is associated with ( ![]() ) and 0 at
all other nodes (
) and 0 at
all other nodes ( ![]() for
for ![]() ). Because
the Galerkin approximation must hold for all
). Because
the Galerkin approximation must hold for all ![]() , let
, let ![]() consist of all linear combinations of functions in
consist of all linear combinations of functions in
![]() . That is,
. That is,
![]()
where the ![]() 's are unconstrained except for homogeneity
constraint on
's are unconstrained except for homogeneity
constraint on ![]() which requires that
which requires that ![]() for nodes on the
dirichlet boundary (
for nodes on the
dirichlet boundary ( ![]() ). The trial solutions will be
drawn from the same basis, leading to
). The trial solutions will be
drawn from the same basis, leading to
![]()
where ![]() for nodes on the
dirichlet boundary. Finally, note that this set of basis functions
is only spatially varying. This leads to the following form for
for nodes on the
dirichlet boundary. Finally, note that this set of basis functions
is only spatially varying. This leads to the following form for
![]() .
.
![]()
Replacing the appropriate functions in (G) will produce a nonlinear system of ordinary differential equations.
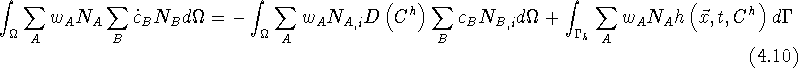
Linearity of integration allows the exchange of the integration operator with the summation operator, giving
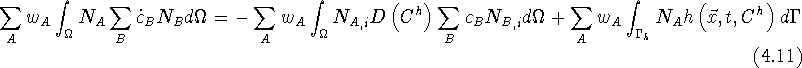
or
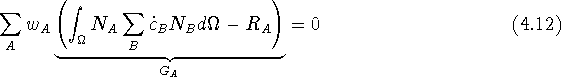
where
![]()
Because the ![]() 's are unconstrained (for
's are unconstrained (for ![]() ),
each corresponding
),
each corresponding ![]() must be 0.
must be 0.
![]()
for ![]() .
.
At this point, the use of Einstein notation becomes cumbersome and confusing so we return to the gradient notation. This equation is
or, with ![]() and
and ![]() , 4.15 can be rewritten as
, 4.15 can be rewritten as
This is a system of nonlinear ordinary differential equations which can be solved using ODE techniques.