Tao Chen's Page

Hello, welcome to my home page!

Currently, I am doing research in automatic mesh generation and related device and process simulations. My program CAMINO (Cardinal's Advanced Mesh INnovation with Octree) is a 3D/2D meshing program using a generalized octree/quadtree approach. However, there is a major difference between CAMINO and other octree/quadtree or 2-4-8 tree programs. We try to match the exact geometry boundary with our generated mesh while most other programs try to perturb the geometry to fit the octant boundary for easier tetrahedralization afterwards. Our philosophy is that we feel every small feature presented in the geometry is important. And reasonable simulation difference will result if they are not captured properly by the mesh program. (you don't want to waste your effort doing all those etching/deposition, just to have your mesh program perturb the geometry later for device simulation, do you?) As you can imagine now, the tetrahedralization in our approach is a very nasty job since we need to match all kinds of geometry while also keeping the mesh comformality along the octant boundaries. Fortunately, now I have finished the mesh program and am constructing a server to be used for device and process simulations.

Generalized Octree Mesh Algorithm

Regular 3D gridding algorithms often generate a very large amount of mesh points due the complexity of 3D doping profiles and 3D geometry structures. The generalized octree algorithm tries to handle that problem by refining in different directions and in various regions. A vector level control function is defined on the domain and used to determine whether or which direction to refine a particular octant. Basically, an integer valued 3D vector function (Lc) is defined on the solid volume. Every octant also has a level vector (Loct) indicating its position in the tree. By comparing Loct and Lc evaluated on the octant, one decides how the octant is refined. It could be one of the following eight situations (refinement in x, y, z, xy, xz, yz, xyz, or no refinement).



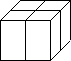
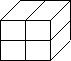
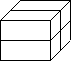
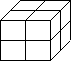
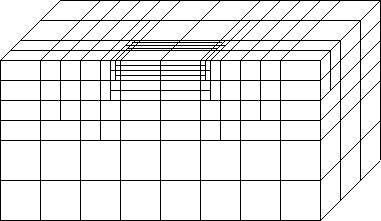
To abide by the one level difference rule, for every octant refined, all its neighbors are found through the tree structure and updated. The level control function increases its values on the neighboring octants if necessary so that there is at most one level difference in every direction between two adjacent octants. The following is a simple generalized octree and mesh illustration.

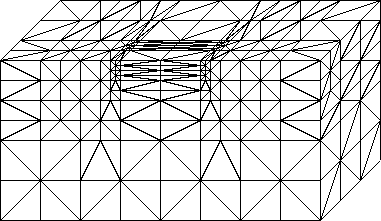
After the tetrahedralization, we apply the following local topological Delaunay transformation to improve the mesh quality. Analogous to the 2D edge swapping algorithm, we substitute two tetrahedra not satifying the Delaunay criteria with three, and vice versa. With an iterative sweep over all tetrahedra, and when it converges, a Delaunay tetrahedralization will result.

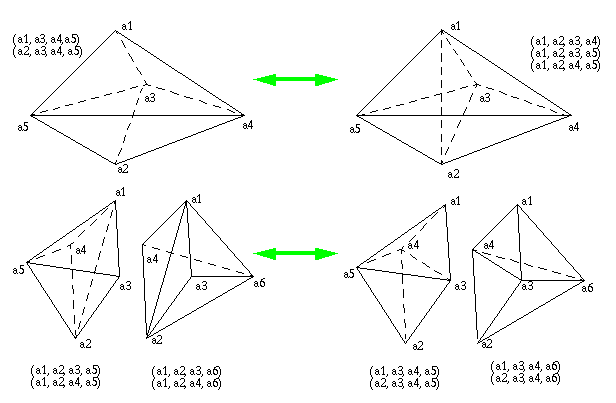
Reference

  • A Vector Level Control Function for Generalized Octree Mesh Generation . (SISDEP/SISPAD'95), - Chen, Johnson, Dutton.

    Basic Functionalities of CAMINO

    Example 1

    The following is a BJT used in an Ericsson high frequency, high power, radio communication circuit. It has 3 bases, and 2 emitters. As shown in the mesh, most of the grid points are concentrated along the junctions.

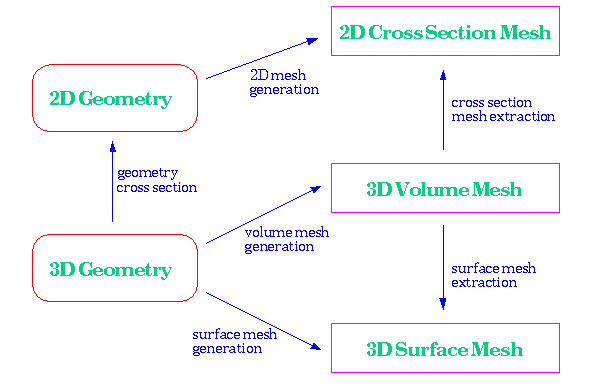
    2D cross section of the mesh and its zoom in view.

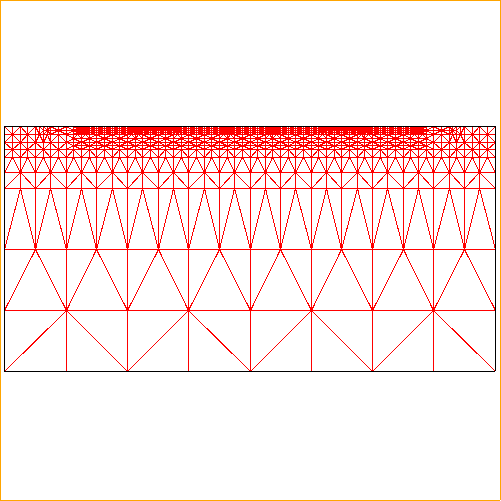
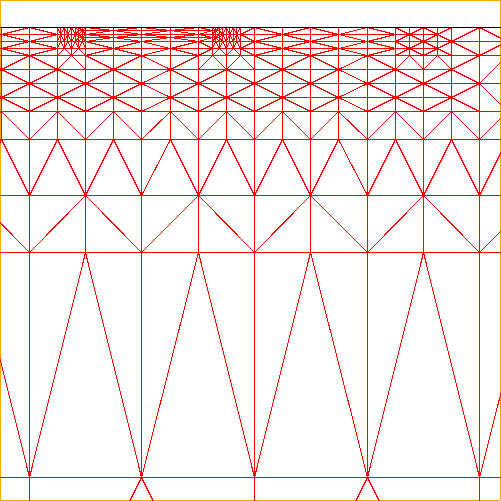
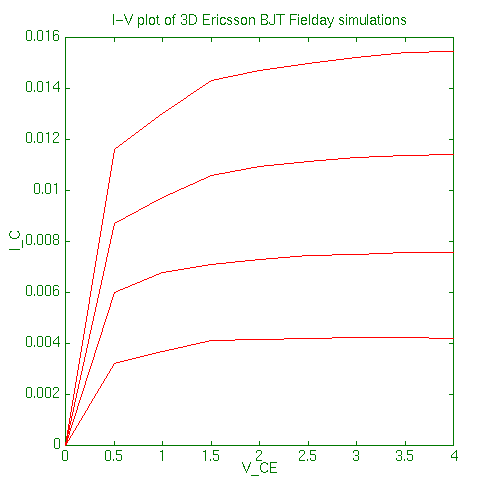
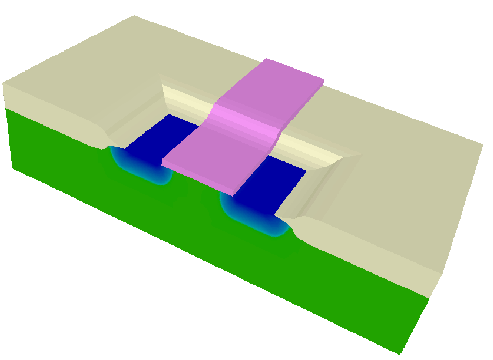
    Some IBM FIELDAY 3D device simulation results of the BJT.

    :

    Example 2

    The following is a MOSFET with complicated geometry. It's generated using our group's vip3d program which takes a 2D SUPREM simulation result and produce a 3D solid model. The birdsbeak has about 8 faces each side. CAMINO automatically tracks the geometry and decide which directions to refine to best fit to birdsbeak. As shown in the mesh, CAMINO also refines along the junctions. The simulation results will come soon!

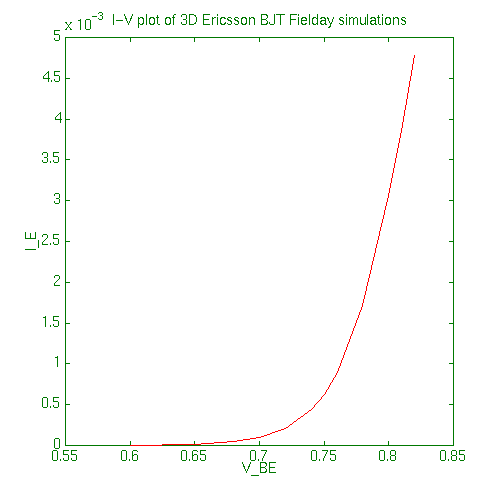    , the way to go!