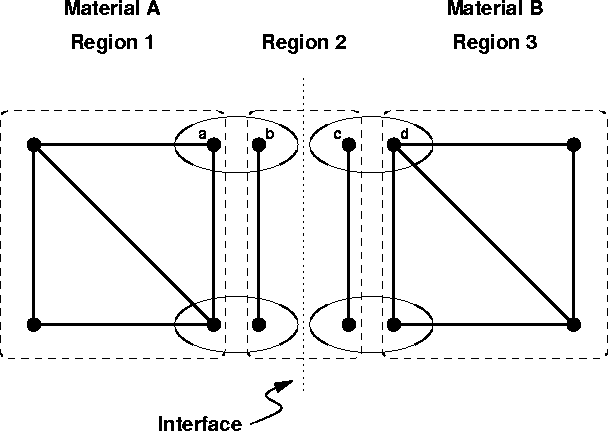
Figure 1: Partitioning of a mesh and representation of discontinuity at a boundary
Daniel W. Yergeau and Robert W. Dutton
Stanford University
Alp H. Gencer and Scott Dunham
Boston University
The ``scripting'' of physical models has evolved over the past decade, both for ECAD and TCAD models, from simple parameterization of fixed models towards user-defined models. This white-paper project is exploring the options for a common (and hopefully minimal) diffusion model representation that would allow model developers to script models using a simple language outside and independent of the simulators that execute the models. The common representation would provide for rapid transfer from model developers (i.e. university researchers), who would produce and distribute their models in the format discussed below, to industrial end users, who could immediately apply the model to simulation of dopant profile evolution in a device structure using a conforming TCAD platform.
The primary limiting assumption is to restrict applicability to continuum PDE-based models appropriate for simulation of redistribution of impurities in orientation-independent materials. The intent of this paper is not to propose an environment capable of simulating every ``diffusion'' mechanism imaginable, but rather to produce a realistic and useful environment for portable diffusion model representation and simulation applicable to bulk processing for silicon technology.
The hierarchy of diffusion models targeted by this representation ranges from the ``fermi'' model, in which excess point defects are ignored and diffusivities are only functions of the local Fermi-level, through the ``fully-coupled'' model, in which excess point defects and extended defects are considered and dopant-defect pairs are considered to be in equilibrium with the local dopant and defect concentrations, to kinetic models, in which the assumption of local equilibrium of pairs is removed and dopant-defect complexes are solved for as independent variables.
These diffusion models can also be influenced by stress and moving interfaces caused by concurrent oxidation or salicidation processes. The equations that are used to model these external processes cannot be represented by the proposed scripting specification discussed in this paper, but the impact of these loosely coupled effects on the diffusion equations can be included in diffusion models by staggering the simulation of the script-based diffusion model with the simulation of the concurrent process via an non-script-based model available in the simulator and the sharing of field data, such as the speed of the moving boundary.
Future revisions of the specification for this environment will likely address issues such as orientation-dependent diffusivity and may even extend the model representation to include PDE representation into the continuum mechanics realm with applicability to oxidation/salicidation as well as thermal stress modeling.
While simulators providing only prepackaged ``general'' models, such as the fully coupled formulation, may look promising as the foundation for a prototyping environment, it is important to note that effects such as TED caused by dissolution of [311] defects, in order to be be predictively modeled, require additional equations. With the traditional approach to implementing process simulators, the discretized equations and intelligence about when to add extra equations/terms is hard-coded in the simulator. Access to and an understanding of the source code would normally be required to prototype a new model. There are quite a few reasons why the implementation approach must be changed. The most significant ones are:
The simulation environment must support discretized solutions of user-specified PDE-based models. This requirement means that the simulator must provide enough intelligence to map a PDE-based description into a discrete system of equations to be solved during simulation of the profile evolution. The discretization approach to be implemented (e.g. semi-discrete finite elements or box integration) will not be specified, but it is expected that the simulation environment will provide appropriate and robust spatial and temporal discretizations and include at least temporal error control, if not also spatial error control.
Although a ``wafer representation'' is a critical building block for any process simulation tool, a large list of restrictive requirements is not necessary to support a rapid prototyping environment. Mesh and field representation requirements will be presented rather generically. There are only a few essential features needed to support portable model representation.
There is a mechanism in the model description to specify continuity across an interface, when continuity is required for the model.
Figure 1: Partitioning of a mesh and representation of discontinuity
at a boundary
In addition to the mapping of the PDE-based description, a few additional capabilities are also needed. These include:
The ``models'' to be represented are multi-region, arbitrarily coupled systems of scalar PDEs. A scripting language will be used as a portable representation. Desired characteristics include:
The same model should be usable on a 1D, 2D, or 3D device structure.
It should be possible to reference an existing model and add terms/equations to a model without respecifying the entire model.
The semantics for mapping a model representation into a discretized system of equations should allow for the discarding of terms and equations related to unavailable solution variables, materials, and interfaces. This mapping includes creation and initialization of auxiliary solution variables as needed by the model.
The representation should not contain non-essential characteristics that tie its use to a particular simulation environment.
There are a few dial-an-operator
diffusion simulators
that provide for specification of fairly arbitrary PDEs to be used
as diffusion models (ALAMODE [5], DOPDEES [1],
PEPPER [3], and PROPHET [4]). Each of
these can represent and simulate general diffusion models within the
limitations of the available terms in their ``operator'' libraries.
Each supports specification at a script level as a multi-region,
arbitrarily coupled systems of scalar PDEs. None of these has a
native scripting representation that satisfies all of the above
characteristics.
Both DOPDEES and ALAMODE have structure query mechanisms, and can produce a mapped model via their TCL front-ends based on the available fields, materials, and interfaces.
There is an effort under development to produce a format (Process Modeling Modules [2]) that can be shared by DOPDEES and ALAMODE. The present implementation reflects limitations from both DOPDEES and ALAMODE.
shows that
a diffusion model is composed of a list of systems of
equations and, optionally, boundary conditions (Dirichlet
and/or continuity constraints). Each system of equations
composed of a list of equation to be applied in a
region. Each equation is composed a of sum of terms,
and it solves for an interpolated solution variable.
Evaluables, parameters, and functions provide the
building blocks for terms.
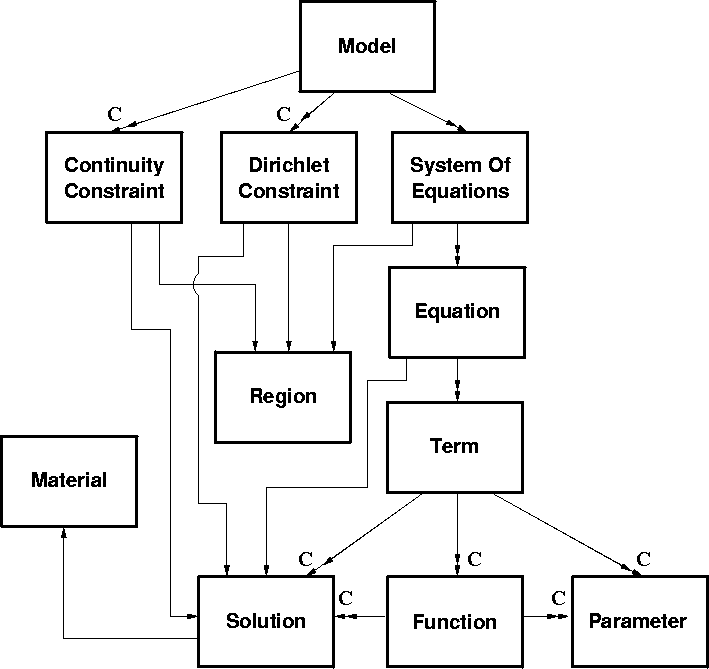
Figure 2: Entity-relationship diagram for a PDE-based model
representation
Because solutions are assumed to be discontinuous at material interfaces, there needs to be a way to distinguish the values on either side of the interface. Adding a material key to the solution will uniquely identify values on either side of the interface. For references to solutions in bulk material regions, the material key is redundant, but the redundancy doesn't lead to any problems.
The components are defined as follows:
Note that both bulk material regions and interface regions are treated homogeneously. This is a very important characteristic. The information model does not differentiate between equations (or terms) that are in bulk materials or interfaces.
Although the ER diagram is useful for documenting the information model, it does not imply a unique scripting language representation. The ``to-many'' relationships from term is an ordered argument list, and it will have a fixed number of slots for each type of term. The ``to-many'' relationships from function represent a general algebraic expression, and this would ideally be described as an expression grammar. The remaining ``to-many'' relationships are unordered lists.
The acyclic structure of the ER diagram implies that an ordered (bottom-up) syntax can be used for construction of models. The various lists will be implicitly constructed, rather than explicitly enumerated, in order to best meet the desire for hierarchical description.
The scripting language proposed here is an extension of TCL, and it provides for
The additional TCL commands implementing the proposed script-based representation are given in the following sections.
alias solution <name in model> <name in simulator>
alias material <name in model> <name in simulator>
The alias statement sets up a one-to-one global mapping between solution and material names used in the model description and those provided by the wafer representation database in a simulator.
The mappings provide for portability of the model description without specification of a standard set of names to be used for solutions (dopants, defects, clusters, etc.), and materials. Specifying a standard set of names would limit portability to the names in that set.
region exists <region name>[@<instance name>]
region current <region name>[@<instance name>]
If exists is specified, then the wafer database is queried. The return value is "0" (TCL false) if the region does not exist and "1" (TCL true) if the region does exist.
If current is specified, the current region is set to to <region name>. The current region is needed to implicitly build up the lists of terms and equations. This must precede the first parameter, solution, term, or function statement.
If an @<instance name> is provided, then the following parameters, functions, and terms are only applied to the specified instance of that region, and any future region default region specifications will be ignored for that instance. Note that this does not imply that any parameters, functions, and terms added to the specified instance before the first occurrence of region current with the @<instance name> will be deleted. If the intent is that the region tagged with @<instance name> will have a unique model, the @<instance name> should be specified before any regions with the same <region name> .
The <instance name> is a non-portable feature that is intended only to aid integration with existing process simulators by avoiding the requirement of new material types for each region where the equations may be different. As an example of the intended use of @<instance name>, consider a SOI structure in which it is desired to use an advanced TED model in the isolated device structure and a simplified equilibrium model in the rest of the substrate. The @<instance name> provides the selection mechanism for deciding which model will be applied in the otherwise indistinguishable silicon material regions.
The <region name> should be the same as the <material> for bulk regions. For interface regions, it should be a concatenation of the two <material> names separated by a forward slash (/). The order of the two names is not important. MaterialA/MaterialB equivalent to MaterialB/MaterialA.
solution exists <solution name>[@<material>]
solution dirichlet <solution name>[@<material>]
solution continuous <solution name>
solution create <solution name>[@<material>] <function tag>
If exists is specified, then the wafer database is queried. The return value is "0" (TCL false) if if the solution variable does not exist in the current region and "1" (TCL true) if the solution variable does exist.
The dirichlet and continuous options are used to set Dirichlet and continuity boundary conditions for the specified solution variable. The @<material> qualifier should not be given for continuity constraints in an interface region, but it should be specified for Dirichlet constraints, unless the interpolation values on both sides of the interface are fixed.
The create option specifies that the solution variable is to be created if it does not exist in the wafer representation. The function referenced by <function tag> is used to initialize the solution variable's values.
parameter defined <parameter tag>
parameter <parameter tag> {<parameter expression>}
If defined is specified, then this command returns "0" (TCL false) if the parameter has not been defined in this region and "1" if the parameter has been defined.
The parameter statement defines a parameter that can be used later in a model and provides an expression for evaluating it. The expression may include references to other parameters (including the predefined parameters, TEMP_K (temperature in Kelvin), TEMP_C (temperature in Celsius), TN, and DT, which reference the simulation temperature, time at the start of the integration interval, and time step for the integration interval, respectively). The expression is a C-style expression, limited to the following operators:
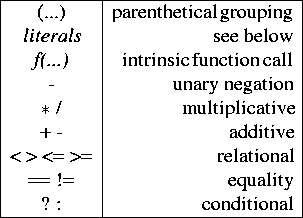
A literal is a numeric constant, a <parameter tag>, a TCL variable substitution (i.e. $varname), or a TCL command (e.g. [expr ...]) substitution. If a TCL substitution is present, it is evaluated once, at the time the parameter statement is processed and cannot reference other parameters.
The intrinsic function set is the same as those listed for the function statement minus the coordinate access functions.
Dependence on time and temperature is handled by the simulation environment, and parameters are reevaluated as needed using the supplied expression.
The numbers referenced as parameters will have an assumed unit set associated with them. The set of units must be self-consistent within the model and consistent with the discretization units in the simulation environment. For the simulation environment, the recommended standard for a set of units assumed for quantities supplied by the simulation environment is:
The <parameter tag> name-space is per-region, not global.
term <solution name>[@<material>] +/- <term name> [<arg> ...]
This statement specifies a term to be added to the equation solving for <solution name>[@<material>] in the current region. The material need not be specified for bulk regions.
The +/- indicates whether the term should be added to or subtracted from the equation. For all equations, the sum of the terms equals zero.
A minimal set of terms and their arguments is listed below. Unless otherwise specified, each of the arguments can be a <parameter tag>, a <function tag>, or <solution name>[@<material>].
Adds the scalar quantity given by <S> to the equation.
Adds a discretized diffusion term ( 
) to the
equation. <D> is the diffusivity, and <C> is the
migrating species.
Adds a discretized drift flux term to the equation. In typical diffusion models where the drift term is given by
<M> would lump the charge, mobility, and active concentration, and <P> would provide potential.
Although this operator looks equivalent to the diffusion operator, this separation allows for a stabilized discretization (e.g. via upwinding).
Adds a first order transient term to the equation. Only one first order transient term can be specified for each equation. Note, also, that this is not a general time derivative on a function. It can only be applied to the solution variable being solved for by this equation.
These are used to set the sign convention for interface flux constraints and can only be specified for interface equations. Only one of these or a d_dt term can be specified for an interface equation. The in or out convention is defined by the material specified for the solution variable being solved for.
function <function tag> {<function expression>}
The function statement defines a function named <function tag> which is evaluated by the given expression. The expression is a C-style expression, limited to the following operators:
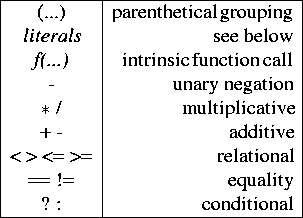
A literal is a numeric constant, a <parameter tag>, a <solution name>[@<material>], a <function tag>, a TCL variable substitution (i.e. $varname), or a TCL command (e.g. [expr ...]) substitution. If a TCL substitution is present, it is evaluated once, at the time the function statement is processed and cannot reference parameters or functions.
The required set of intrinsic functions is:
Implementations may provide intrinsic functions beyond those required here, but scripts that make use of those are not guaranteed to be portable among simulators.
The mesh coordinates returned have the default discretization units.
The <function tag> naming/access mechanism does not provide for function definitions with replaceable arguments.
To validate an implementation, a suite of TCL scripts should be developed to test all forms for each of the additional TCL commands as well as ensuring a correct implementation of expression syntax and availability of the required intrinsic functions. The expression validation tests can be performed using the solution create command.
Validation of the numerical discretizations can be performed by using models with known analytic solutions and measuring the error between the simulated results and the analytic solutions. Examples of test cases include a static homogeneous Poisson solve in 1D with Dirichlet boundary conditions or a transient linear diffusion simulation with an initial 1D Gaussian profile which would produce a Gaussian profile as the final result.
The emphasis in the preceding discussion has been to present sufficient descriptive capabilities to represent the PDE-based models required for simulation of orientation-independent ``diffusion'' processes in semiconductors. There is also a number of more pragmatic requirements that may still need to be considered.
Many of the diffusion models will produce updated solution variables that are not immediately usable or even understood by other TCAD simulators, such as device simulators. Fixed model simulators know how to postprocess their fixed set of solution variables (e.g. active and chemical dopant concentrations) into a variable such as a net active concentration profile that a device simulator requires. The heuristics for postprocessing arbitrary solutions variables into a form that makes sense for another TCAD simulator are determined both by the semantics of the solution variables as calculated by the model and by the data input requirements of the next simulator in the chain. The latter makes it impossible to portably add postprocessing capabilities as part of the portable model description, but a capability similar to the solution create would be useful as a mechanism to provide postprocessing.
Another benefit from including some portable postprocessing is to help to meet validation needs, both validation of conformance of the environment as well as validation of model scripts. Profile extraction and plotting should be provided. The ability to compute integrated quantities (e.g. total integrated dose or the integral of an arbitrary function) are very useful for model validation.
The fact that end users can specify and/or change parameters, terms, and equations in the model may be unsettling to managers who only want a specific model and parameter set to be used for simulation. Fortunately, disabling these capabilities is trivial in TCL. Any TCL command can be disabled by redefining it at the script level. For example, proc region {} {} could be executed after the model definition phase to disable the region command.
In order to have confidence that the computed results are a reasonable approximation to solution of the systems of equations, the error in those computed results should be controlled by user-specified error control parameters. Because these meaning of these error control parameters will vary, depending on the approximations used to estimate them, they cannot be part of the model representation. It is expected that all simulation environments will provide per-field relative error control parameters for control of temporal error (e.g. control timesteps such that less than 1% relative error is introduced as a result of time integration). Error control parameters related to control of spatial error are less standardized, and no recommendations are made on these.
The dial-an-operator abstraction discussed here is based on linearly independent terms contributing to equations and also on scalar expressions. This level of abstraction was chosen because it is the level of abstraction used in the prototype dial-an-operator codes, ALAMODE and DOPDEES, and because it is sufficient for representation of diffusion models. The level of abstraction could have been moved closer to the mathematical operators that make up the terms described above. For example, instead of providing diffusion and drift terms, a vector/tensor field concept could have been introduced along with the mathematical operators (e.g. divergence, gradient, and an ``upwinded'' gradient, or even down to individual d_dX, d_dY, and d_dZ operators) to create and reduce flux components. Thus, instead of writing
term C + diffusion D Cone would write
term C + {div(D grad(C))}
The benefit of this alternative representation format is that it has more expressive capabilities and it is likely that a wider range of TCAD models could be described (e.g. stress-strain equations and orientation-dependent diffusivities). The main drawback is that existing codes such as ALAMODE, DOPDEES, and PROPHET would likely need significant rework to be able to accept and solve models described in the alternative mathematical format. Also, models that are described in the original format should be able to be automatically converted to a format supported by an environment providing a more mathematical representation.
A model implementation environment to support
rapid prototyping of new TCAD models:
A case study for dopant diffusion
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -no_navigation -split 0 -show_section_numbers -no_reuse sematech.
The translation was initiated by Dan Yergeau on Tue May 5 10:15:59 PDT 1998