Computational Time

Costs and Benefits

The two level Newton method for mixed circuit/device simulation incurs a significant computational cost. Mayaram had investigated that cost for a variety of algorithms including the two level Newton [3]. The most common of the alternate algorithms is the full Newton which Rollins had implemented previously [4].

In the full level Newton algorithm, the circuit matrix and device matrix are combined into a single matrix and all variables are solved simultaneously. As a result, the computational time is reduced, but there are trade-offs.

The two level Newton algorithm has the following advantages:

1. It has better convergence for DC analysis if node voltages are unknown. The full Newton requires all circuit node voltages to be specified within a certain percentage; otherwise, it fails to converge.
2. The modularity in two level Newton allows many device simulators to be used simultaneously. For example, PISCES may be used for standard devices in the circuit whereas an in house device simulator may be used for novel devices
3. It is easier to implement a parallel version of the two level Newton algorithm. Each numerical device simulation can be relegated to a node of a parallel machine whereas the matrix for the full Newton algorithm has to be partitioned to each node.
4. By utilizing SPICE as the circuit simulator, any improvements/ modifications in SPICE automatically benefit the mixed-mode simulation.

Likewise, there are a number of disadvantages to the two level Newton algorithm:

1. Given a good estimate of all the circuit node voltages, the full Newton algorithm converges more quickly than the two level Newton.
2. Similarly, since transient analysis involves small voltage changes at each time step making the problem well behaved, the full Newton method converges much more quickly for this case as well. Mayaram determined a factor of 1.7 times as fast [3].

Bench Mark Circuit

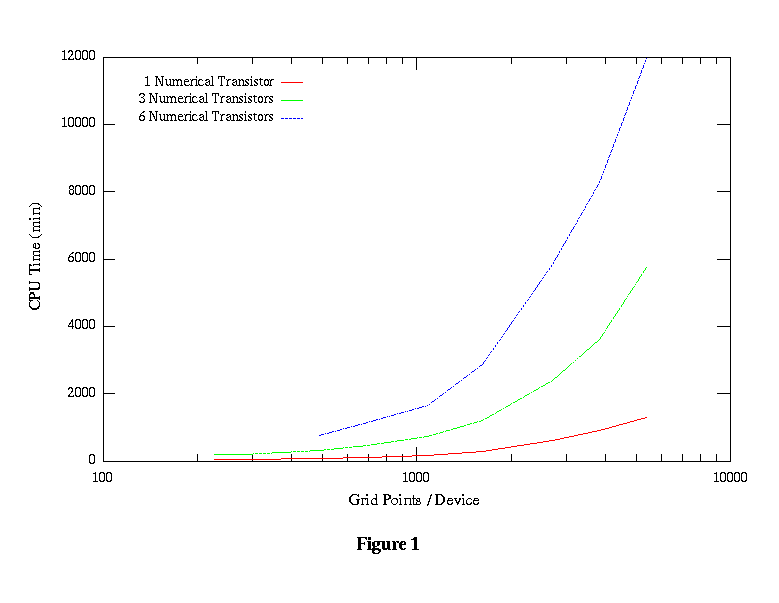
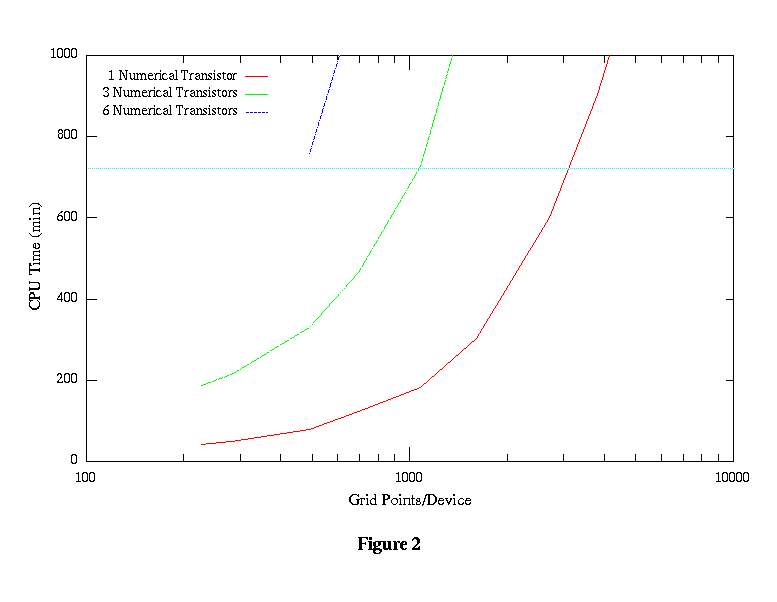
The SRAM example was used to analyze the computational time of mixed-mode simulation. The six transistor SRAM cell is simulated with a set of numerical devices containing a wide number of nodes for each device. In addition, three circuits are simulated. One circuit has only the pass transistor as a numerical device, another has half the cell (3 transistors) as numerical devices, and the third has all six transistors as numerical devices. The circuit was simulated to do a read/write cycle of a one and a zero so that each half of the cell is excersized in the same manner for when we don't have symentry. The non-numerical device transistors are modeled to approximate the numerical device characteristics.

The simulations were executed on a single node of a SP1. The CPU time in minutes is shown in Figures 1 and 2. Figure 1 shows the total time for all the simulation runs. Figure 2 shows those that would take overnight or less with the light blue line representing the 12 hour mark with the fastest time being around 45 minutes. For the 6 numerical transistor circuit with minimal node devices, convergence became a problem and no data is available.

Return to Top