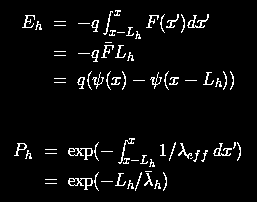
In this project, we first developed the II model for the isotropic band structure using the complete II model for the full band structure of Silicon (See reference [3]). This II model we developed not only preserved the same scattering rate at each iso-energy surface in the first Brillouin zone of the electron momentum space as the full band one but also make the II model consistent with the isotropic band used. By tuning the deformation potentials of phonons, the MC can fit to several experimental data sets, such as drift velocity, II coefficient and quantum yield. Then we use this MC to study and further model the TEHD model under nonhomogeneous (n-i-n structure) as well as homogeneous (silicon bar) electric fields. With proper modeling using a closed set of parameters (e.x. tail electron concentration n2, etc.), we can get the same II generation rate as MC not only in the channel region but also in the drain region where the hot electrons are embedded in the cool electron sea.
In conclusion, the II model of this work uses the results of accurate calculations based on the full band structure in the frame of a more simplified silicon isotropic band structure. This model is able to well reproduce several available experiment data. For TCAD usage, TEHD which is especially useful for hot carrier transport has been developed using this MC model. With proper modeling from MC, TEHD can describe tail electron and II phenomenon as well as MC and it makes TCAD for devices design more reliable and attractive.
The high-energy part of the carrier distribution can be treated
differently from the entire distribution using a perturbation
approach (for a more complete review, see [8] and
references therein). If the mean energy is close to the definition of the
high energy, this treatment is somewhat blurred and questionable.
Nevertheless, from the classical point of view, as long as
the bulk II coefficient is proportional to exp(-C/F) instead of
exp(-C/F^2) where F is the electric field and C is
an arbitary constant, the two-population
description should be more accurate than the one-population model.
The probability Ph of carriers obtaining energy Eh from the electric
field F(x) without losing energy due to scattering can be estimated by
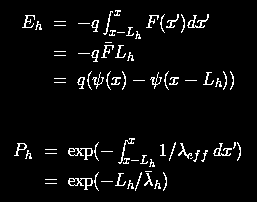
If we assume that hot carriers have an infinite rate to impact ionize once their energy reaches Eth, this is the classical lucky electron model and the nonlocal field (NLF) model in [6], where a 2-D generalization is implemented. This is not to be confused with the lucky electron model in [7], where a specific field profile has been assumed for MOSFET applications. It was thought that energy calculation in of the lucky electron model should start from the average carrier energy related to Tc instead of $0$ to better model the drift and thermionic contributions to hot carriers [5,8]. However, this modification mixes the two-population concept and does not show correct asymptotic behavior. Intuitively, the average carrier energy cannot be added to the hot carrier energy directly since it is randomized with respect to the direction of the electric field.
The infinite II rate beyond Eth however precludes hot carriers with energy larger than Eth (no thermionic gate current in MOSFET). To include a finite II rate, separate population and energy conservation equations can be explicitly solved for carriers with energy larger than a threshold energy [2] as described above in TEHD. However, the tail population is estimated from the Monte Carlo (MC) calculation with some pre-selected matching parameters. The parametrization step from MC, although good for a particular field profile, is hard to be generalized for arbitary applications. To include a soft threshold, the threshold energy of the tail electron model can be pushed below bandgap. This modification is still under investigation.
The local temperature (LT) II model
significantly overestimates
the diode breakdown voltage, while the local field (LF) II model
overestimates MOSFET substrate current.
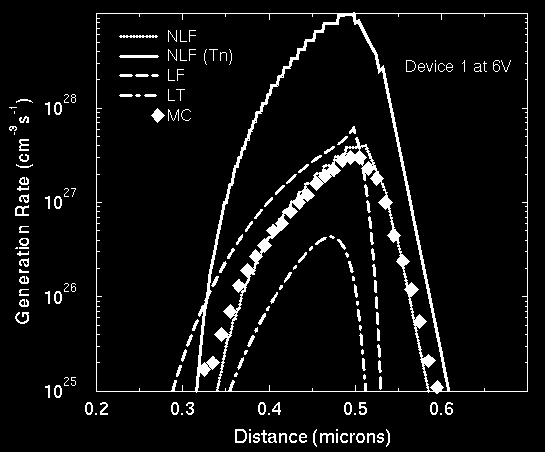
Here we show the generation rate in a 0.4um
nin diode. The asymptotic behavior
of these models in view of the generalized macroscopic model is
described below.
The field variations can be characterized by aF =
|F/dF/dx|. We will first consider only
monotonic profiles of F.
For pn junctions, aF is close to the depletion
region width, which in Si is typically larger than 2000 A before
Zener breakdowns. If aF >> LI, which is around
70-200 A for silicon, the average field in NLF can be very well
estimated by the local field. However,
aF for conventional MOSFETs is much smaller. The apparent success
of the LT model for MOSFETs can be seen from the
approximate solution
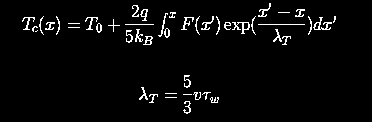
If aT is quite large in comparison with aF and LI,
Tc provides a detour to evaluate the average field in NLF.
If aF >> aT as in pn junctions, II is severely underestimated.
For moderate field variations such as in LDD MOSFET,
adjustment of parameters in LF and LT is necessary and these
models lose their predictivity.
From the asymptotic cases of gradual and abrupt field variations, it is clear that the LT model is valid only because it provides an estimation of the average field, not because it represents also the random part of the mean energy. If the average carrier energy is added directly to Eth, we have double-counted the contribution from the electric fields. This is manifest in the above figure for the nin case, where the field variation can be considered as gradual. When the parameter set of NLF generates good agreement with MC in nin diodes (the same parameter set has been used in LF, LT and NLF to fit the bulk case), the further addition of Tc contribution to Eth will make the generation rate far exceed the results of other models. Even if Eth is tuned to 1.75eV, NLF with T_c addition still predicts much larger generation rate than the MC results.
We have explained the past II models in a unified framework and suggested potential generalized II models. For applications in deep-submicron or high-power silicon technologies, the II model with asymptotic correctness to gradual and abrupt field variations, will greatly enhance the predictivity of device simulation.
References:
[1] C.-S. Yao et al., "Formulation of a Tail Electron Hydrodynamic Model Based
on Monte Carlo Results," Elec. Dev. Lett., vol. 16, no. 1, pp. 26-29, 1995.
[2] J.-G. Ahn et al., "Impact Ionization Modeling Using Simulation of High
Energy Tail Distribution,", Elec. Dev. Lett., vol. 15, no. 9, pp. 348-350,
1994.
[3] C.-S. Yao et al., "An Efficient Impact Ionization Model for Silicon Monte
Carlo Simulation," VPAD93, pp. 42-43, 1993.
[4] A. Abramo, et. al., ``A comparison of numerical solution of the Boltzmann transport equation for high-energy electron transport silicon, '' IEEE Trans. Elec. Dev., vol. 41, no. 9, pp. 1646-1654, Sept. 1994.
[5] K. Hess, Advanced Theory of Semiconductor Devices,
New Jersey: Prentice Hall, 1988.
[6] H.J. Peifer, B. Meinerzhagen, R. Thoma and W.L. Engl,
``Evaluation of impact ionization modeling in the framework
of hydrodynamic equations, ''
IEDM Tech. Dig., 1991, p. 131.
[7] S. Tam, P. Ko and C. Hu,
``Lucky-electron model of channel hot-electron injection in MOSFETs, ''
IEEE Trans. Elec. Dev., vol. ED-31, no. 9, pp. 1116-1125,
Sept. 1984.
[8] B.K. Ridley,
``Lucky-drift mechanism for impact ionization in semiconductors, ''
J. Phys. C., vol. 16, pp. 3373-3388, 1983.
Gyo-young Jin (gyjin@gloworm.Stanford.EDU)